ユニーク&エキサイティング研究探訪
No.09 武田研究室のフーリエ変換法とその応用展開
キャリア縞信号を用いた様々な測定分野で世界的に応用が広がる
情報理工学研究科 先進理工学専攻
武田 光夫 教授
国際光工学会(SPIE)の国際賞である2010年度Dennis Gabor Awardを武田光夫教授(先進理工学専攻)が受賞した(注1)。この賞は、ホログラフィーの発明でノーベル賞を受賞したDennis Gabor博士の功績をたたえて国際光工学会が1983年に創設したもので、光の干渉を応用した計測技術や、ホログラフィー開発などの分野で卓越した研究業績をあげた研究者(毎年一人)に与えられている。今回、賞の対象になったのは、武田教授が1982年に発表した「フーリエ縞解析法」[参考文献1) 以下、フーリエ変換法と呼ぶ]の発明と、最近のコヒーレンスホログラフィーの研究だが、ここではフーリエ変換法に焦点を絞り、原理と応用の一部を紹介してみよう。
通信との類似でヒントを得る
フーリエ変換法は当初、光の干渉縞の空間分布の中に秘められた物体情報を抽出するための「干渉計測法」の1手法として考案された。
測定対象からの光にそれと干渉するもうひとつの基準となる光を重ねると、そこに干渉縞が出来る。その縞を解析することで、測定対象の形状や屈折率分布など、さまざまな物理量を計測しようとするのが干渉計測法である。干渉縞の縞模様の明暗分布には、測定対象に関する物理情報が秘められているがそのままでは見えない。フーリエ変換法は、その秘められた情報を、フーリエ変換を用いた縞解析によって高精度に取り出すという技術だ。
武田教授がフーリエ変換法のヒントを得たのは、通信の分野からだという。通信の世界では送信側でキャリア信号に情報を載せて送り、受信側でキャリアを除去して、情報を取り出すのがごく一般的になされている。二つの光が重なってできる干渉縞は疑似的な周期構造をもっている。それを空間的なキャリア信号(空間キャリアと呼んでいる)と見なし、そのキャリア信号が測定対象によって変調された(縞の規則性が乱れた)状態が、キャリアに情報が載ったことに相当する、と発想したわけだ。つまり、これまでの時間信号の通信理論の考え方を空間信号に適用してみたわけだ。
位相に情報が反映される
通信のキャリア周波数(時間キャリア周波数)に相当する概念として、空間キャリアには空間キャリア周波数という概念を導入する。空間キャリア周波数の単位はHzではなく、本/mmである。空間キャリアを作る方法として、武田教授らが採用しているのは、計測に用いる2光束のうちの一方を他方に対して少しだけ傾けて(ティルトさせる)干渉させる方法である(囲み記事1:「光をティルトさせて空間キャリア縞を作る」参照)。
その空間キャリアに測定対象の物理情報を載せるには、測定しようとする対象によってさまざまな工夫が必要だが、立体物の形状計測などの場合は簡単だ。単に物体にティルトされた光を当てるだけで、縞パターンがゆがむ。つまり、空間キャリアの位相が変調され、その位相の中に物理情報が閉じ込められる(囲み記事2:「位相が情報を持つ」参照)。
フーリエ変換法で位相を取り出す
それでは、空間キャリア縞に載っている位相情報を、どのようにして取り出すのか。図1は、フーリエ変換法の位相検出アルゴリズムを示したものである。
最初に、被測定対象に前述の2光束の光を当て、その表面にできる縞パターンをカメラ(イメージセンサ)で撮影する(図1の左上)。この縞パターンは、
![]() ・・・・・(1)
・・・・・(1)
という数式で表される。ここで、a(x,y) は2光波の強度和から成る項で、干渉縞のバックグラウンド強度分布をあらわし、b(x,y) は干渉縞の明暗変化の振幅をあらわす。φ(x,y) は被測定物体の形状や屈折率分布などの物理量に関する情報を持つ位相分布、![]() はそれぞれx方向、y方向の空間キャリア周波数(単位は本/mm)である。
はそれぞれx方向、y方向の空間キャリア周波数(単位は本/mm)である。
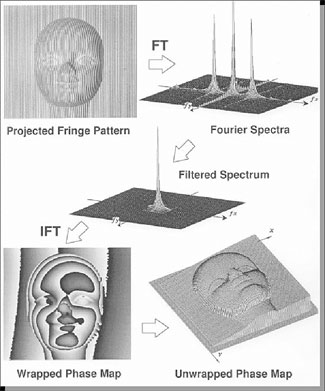
- 図1.フーリエ変換法の位相検出原理
カメラからコンピュータに取り込まれるのは、(1)式のg(x,y) の値であり、それをもとに(1)式を2次元フーリエ変換する。すると、同図右上に示すような2次元空間周波数スペクトルが得られる。このうちの一方のスペクトルは干渉縞の明暗変化の複素振幅
![]() ・・・・・(2)
・・・・・(2)
のフーリエスペクトルあらわしている。それをコンピュータ上で原点に戻す操作を行い、キャリア周波数![]() を取り除き、それをもとにフーリエ逆変換することで(2)式を求める。(2)式が求められれば、その複素対数をとれば、
を取り除き、それをもとにフーリエ逆変換することで(2)式を求める。(2)式が求められれば、その複素対数をとれば、
![]() の実部から縞の振幅情報が、虚部から位相φ(x,y) を求めることができる、というのが概略の原理である(より詳しくは、囲み記事3:「フーリエ変換法の実際」を参照)。
の実部から縞の振幅情報が、虚部から位相φ(x,y) を求めることができる、というのが概略の原理である(より詳しくは、囲み記事3:「フーリエ変換法の実際」を参照)。
実際には、高速フーリエ変換(FFT)で測定対象のすべての点(x,y)について位相を計算することになるが、計算で得られる位相値は-π~πの間の値をとり、位相値が±πの範囲を超えると、同図左下のように2πの段差をもって不連続に折りたたまれた結果が出てくる。それをアンラッピング処理(位相を2π足したり引いたりする)して、位相をつなぎ合わせて右下のような立体形状の情報を再現できることになる。
広がる応用分野
フーリエ変換法は、冒頭のように「干渉計測法」の1手法として開発された。このため当初は、フーリエ変換法が開発される以前から広く使われている時間キャリア周波数ヘテロダイン干渉計測法(用語説明参照)と相補的な「干渉計測法」の1方法と見なされていた。しかし、「空間的キャリアであれ時間的キャリアであれ、キャリアに載っている情報をフーリエ変換によって他の不用成分から分離して取り出す」というのが、この発明の原理であり、本質である。武田教授は「単なる干渉計測法の一つであるというよりも、むしろ規則的な周期構造(キャリア周波数)が何らかの情報により変調されている時空間縞信号から位相と振幅を抽出するための簡便かつ強力なアルゴリズムと考えるべき」と言う。この本質の理解が進むにつれ、産業計測から極限計測まで、世界中でいろいろな応用開発が進められている。
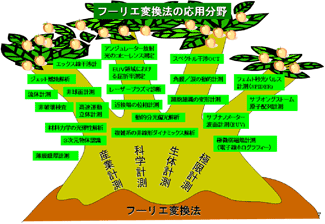
- 図2.フーリエ変換法の応用分野
図2はフーリエ変換法の主要な応用分野を示す。これは最初の論文(文献1)を引用した論文1,400件の中から、応用例を武田教授らが選び出したものである。
初期の応用としては、3次元形状計測が代表例で、フーリエ変換法の原理に基づく3次元形状計測機が日本のOPTON社などから製品化されている。OPTON社の製品は改良が続けられ、現在も自動車産業や航空機産業で使われているという。
最近では種々の極限計測でフーリエ変換法が重要な役割を果たしている。図2に示すように、電子線ホログラフィとフーリエ変換法を組み合わせた極限磁場計測、次世代の半導体露光装置の核になる極紫外光リソグラフィ光学系のサブナノメートル絶対波面計測、ナノデバイスなどに用いる結晶の格子欠陥や格子歪をサブオングストロームの精度で計測する原子格子歪計測、フェムト秒光パルスの振幅/位相計測等々、次世代技術の急所に応用されている。
武田教授らがフーリエ変換法の論文を発表した1982年当時は、この技術はほとんど注目されなかったという。当時のイメージセンサは最も画素数が多いものでも100×100画素で、空間分解能、感度均一性などが十分でなく、値段が150万円もし、おまけにFFT計算するコンピュータの性能も低かったためである。その後の半導体技術およびコンピュータ技術の進歩がフーリエ変換法に対する評価を大きく変えた。
フーリエ変換法の本質は空間キャリア縞信号に限らず、時間キャリア縞信号や時空間多次元キャリア信号にも適用できることだ。応用範囲はさらに広がりそうだ。
(2010年11月)
- 参考文献
1)M. Takeda, H. Ina and S. Kobayashi, “Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry,”J. Opt. Soc. Am. Vol. 72 (1), pp. 156-160 (1982).
- プロフィール
-
武田光夫教授は本学電気通信学部電波工学科の出身。東大大学院修士・博士課程を修了した後、キヤノン(株)で干渉計測や光学設計の研究開発にたずさわった経験がある。電通大に赴任したのは1977年。助教授時代に文部省長期在外研究員としてスタンフォード大学でフーリエ光学で著名なグッドマン教授と共同研究を行う機会を得たのもその後の研究に役立っているという。
フーリエ変換法を思いついたのは「通信分野になじみある電通大の出身者として、ごく自然なこと」と本人は謙遜するが、光の干渉縞を見て、フーリエ変換で情報を取り出そうという発想は、非凡だろう。
ともあれ、1982年に米国光学会誌に発表したオリジナルの論文(参考文献1)、およびその翌年発表した3次元立体計測に関する論文は、現在までに合計2000件を超える世界中の論文に引用され、90年の歴史を持つ米国光学会誌に発表された論文の中では史上6番目に引用件数が多いという(注2)。世界中でそれだけ多数の応用開発がなされたということだ。武田教授自身、現在も国内企業や他大学との共同研究など、最先端の応用開発に取り組んでいる。
- 言葉の説明
時間キャリア周波数ヘテロダイン干渉計測法=レーザー光を2分して2光束を発生させ、そのうちの一方を基準光、もう一方を被測定物体に当たる信号光として干渉させて両者の位相差を検出する。その際に,一方の光束の周波数を光変調素子などで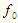 だけずらしてビート(うなり)信号を作り、位相情報を取り出す。ビート信号は光検出器で直接検出可能な周波数
だけずらしてビート(うなり)信号を作り、位相情報を取り出す。ビート信号は光検出器で直接検出可能な周波数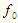 の正弦波になるので、時間軸上で両者の位相差を容易に検出できる。ただ、周波数ヘテロダイン干渉計測法は、基本的に点計測なので、広い面を計測するには、点計測を何度も繰り返さなければならない、といった手間がかかる。また、瞬間的な高速現象の計測には向かない。さらに、電子線波やX線波のようなレーザー光以外の低コヒーレンス波の場合は、周波数ヘテロダインを行うことが難しい、などの制約がある。
の正弦波になるので、時間軸上で両者の位相差を容易に検出できる。ただ、周波数ヘテロダイン干渉計測法は、基本的に点計測なので、広い面を計測するには、点計測を何度も繰り返さなければならない、といった手間がかかる。また、瞬間的な高速現象の計測には向かない。さらに、電子線波やX線波のようなレーザー光以外の低コヒーレンス波の場合は、周波数ヘテロダインを行うことが難しい、などの制約がある。
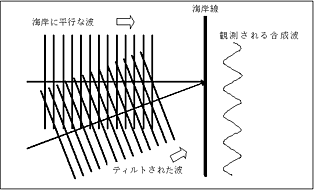
- 図A.傾きのある(ティルトされた)波を加えて干渉させて空間キャリア縞を形成。
- 囲み記事1:
光をティルトさせて空間キャリア縞を作る -
よく知られるように、周期が同じ二つの波が重なると干渉が起きる。二つの波の山と山が重なれば強められ、山と谷が重なれば相殺される。いま、図Aのように海岸で、打ち寄せる波を観測しているとしよう。海岸に平行な波だけなら、ある瞬間に海岸に打ち寄せる波の高さは一定である。ところがもし、それと少し違う角度からもう一つの波(ティルトされた波)が来ると、干渉が起こり、二つの波の山は強め合い、山と谷はキャンセルされる。この結果海岸線にそって正弦波のような波の強弱分布が来ることになる。
光も波なので、同じことが起こる。図Aの海岸線の位置がスクリーンだとすれば、スクリーンに垂直な光だけなら、単に明るくなるだけだが、それとわずかに傾いた方向からもう一つの光を加えると、スクリーン上には明暗の規則正しい縞模様ができる。それが空間キャリアに相当する。ティルトの角度を変えると縞の間隔が変わる、つまり、ティルトの角度調整で空間キャリア周波数を変えられることができる。実際には、一つのレーザー光を二つに分けて、集光レンズと逆の原理で光束を広げた二つの平行光の一方をティルトして照射して、縞パターンを得ている。
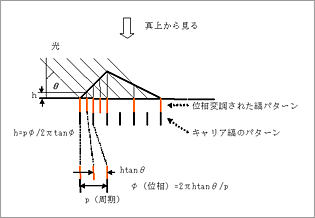
- 図B:位相に情報が載る仕組み
- 囲み記事2:
位相が情報を持つ -
いま、図Bのように、テーブルの上に三角形の物体を置き、それに平行縞パターンを投影することによりこの形状を計測することを考える。このような平行縞パターンは図Aの場合のようにテーブルに垂直な光とそれ対して傾いた(ティルトした)光を干渉させても発生させることができるが、ここではもっと簡単に液晶プロジェクタのようなもので、縞パターンを角度θ方向から斜め投影している場合を考えよう。光の進路に何もなければ、平らなテーブル上には位相がそろった並行キャリア縞パターンができる。その状態でテーブル上に測定対象の三角形物体を置く。それを真上から見ると、図Bのように左半分では密な縞が、右半分では疎な縞模様が見える。物体によってキャリア縞が位相変調されたことになる。つまり、三角形という測定対象の情報は、縞パターンの位相の中に反映されたことになる。
たとえば、対象となる三角形物体のある点のテーブルからの高さhを計測したいとする。投影する光の角度をθは既知だから、位相φが分かれば、物体のテーブルからの高さhは
h=pφ/2πtanθで求められることになる。キャリア縞の周期pは既知であり、pの間に、位相は2π変化するから、その比例関係で、位相φさえ求められれば、高さであるとか、ある位置からのズレなどを、正確に知ることができるわけだ。
- 図C
- 囲み記事3:
フーリエ変換の実際 -
フーリエ変換によって、いかにして位相情報φ(x)をとりだすのか。簡単のために、1次元の場合で話を進めよう。本文で示した2次元の縞パターンの数式を1次元に直すと、次のようになる。
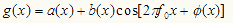 ・・・・・(1)
・・・・・(1)
ここで、a(x) は干渉する2光波の強度の和で干渉縞のバックグラウンド強度分布をあらわし、b(x) は干渉縞の明暗変化の振幅を表す。そして、φ(x)が被測定物体の形状や屈折率分布などの物理量に関する情報を持つ位相である。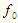 は被測定対象の情報が何も載っていないときの、規則正しい縞模様をあらわす空間キャリア周波数である。周波数の単位は本/mmである。
は被測定対象の情報が何も載っていないときの、規則正しい縞模様をあらわす空間キャリア周波数である。周波数の単位は本/mmである。
フーリエ変換法ではこの(1)式をフーリエ変換することによって、必要な位相情報を取り出す。
ところで、三角関数と指数関数を結び付けるオイラーの公式によれば、
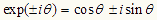
であり、
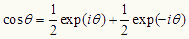
だから、(1)式は、次のように書きかえられる。
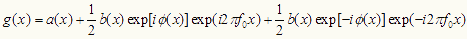
ここで、
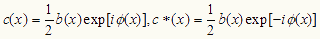 ・・・・・・(2)とおけば、
・・・・・・(2)とおけば、
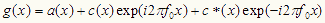 ・・・・・・(3)
・・・・・・(3)
このフーリエ変換は
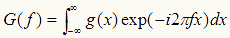
であるから、
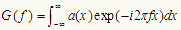
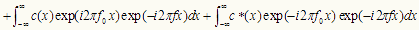
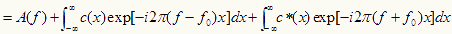
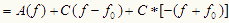 ・・・・・・・・(4)
・・・・・・・・(4)
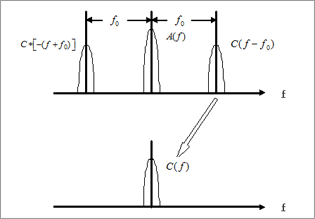
(4)式の第1項は(3)式の第1項a(x) の、第2項、第3項は(2)式のc(x),c*(x) のフーリエ・スペクトルを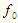 横ずらししたものをあらわしている。式(4)を模式的に示したのが図Cである。
横ずらししたものをあらわしている。式(4)を模式的に示したのが図Cである。
図Cの意味するところは、縞パターンをあらわす関数g(x)をフーリエ変換すると、横軸が空間周波数f の関数G(f )に変換され、それは
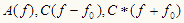 の3つの分離したスペクトルになる、ということだ。
いま、求めているのは位相φ(x)情報 であり、それは(2)式の
の3つの分離したスペクトルになる、ということだ。
いま、求めているのは位相φ(x)情報 であり、それは(2)式の
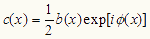 の中に含まれている。
の中に含まれている。
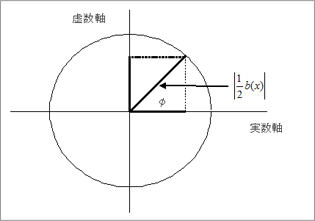
- 図D:複素平面上のイメージ
- 一方のスペクトルを原点に移動する
-
したがって、g(x) 全体ではなく、干渉縞の明暗変化の複素振幅c(x) が分かればよい。そこでc(x) のフーリエ変換である
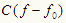 に着目し、これを図C下部のように原点に移動して、その値を使って、今度はフーリエ逆変換してc(x) を求める。
に着目し、これを図C下部のように原点に移動して、その値を使って、今度はフーリエ逆変換してc(x) を求める。
原点に移動するという作業は、空間キャリア周波数を取り除くことに相当する。数式的にはこの操作はしなくてもフーリエ逆変換できるが、この操作をしないとキャリア周波数による位相変化を含んだものが得られてしまい、位相の折りたたみを修復しにくくなるので、実用上は重要な操作だという。いったんc(x)が求められれば、
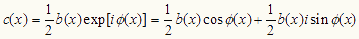 ・・・・(5)
・・・・(5)
であるから、 図Dに示すように、
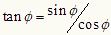 =(5)式の[虚数部/実数部]
=(5)式の[虚数部/実数部]
つまり、φ=tan-1 [虚数部/実数部]で、φ を求めることができる。もちろん、本文のように、式(5)の対数をとる方法でもよい。
- 実現方法
-
実際にはどうするのか。まず、縞パターンをイメージセンサで撮影することになるが、これも簡単のため2次元のカメラではなく、1次元のラインセンサで撮像し、その映像をコンピュータに取り込んだ、としよう。
コンピュータメモリ上では、アナログ情報ではなく、x0,x2,・・・xN-1 の飛びとびの位置でのg(x)の値、つまりg(x0),g(x1),g(x2),・・・g(xN-1)がディジタル情報として格納される。ここでNはコンピュータが計算し易いように通常2のべき乗(512とか1024)に選ばれる。
この値を使って、離散フーリエ変換をする。離散フーリエ変換の式は、
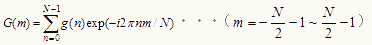
で、これを計算すると、周波数軸上でやはり飛びとびの変換値が得られ、空間キャリア周波数の近傍に、c(x)に相当するスペクトルが得られる。この値をコンピュータメモリ上で原点に移し、その値を使って、今度は離散フーリエ逆変換でc(x)のみを計算する。
その結果、コンピュータメモリ上には、x0,x2,・・・xN-1 の座標に対応したc(x)の値、c(x0),c(x1),c(x2),・・・c(xN-1) が残る。この値は、上記(5)式のようにそれぞれ A+iB のような複素数の形をしているので、それぞれの座標点ごとに位相情報が
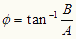 で求めることができる。
で求めることができる。

